智力题：钻石问题 & 爱情问题

有这样一道智力题：

一楼到十楼的每层电梯门口都放着一颗钻石，钻石大小不一。你乘坐电梯从一楼到十楼，每层楼电梯门都会打开一次，只能拿一次钻石，问怎样才能尽可能地拿到最大的一颗？

这道题挺难的。还是先从一道简单点的上手比较好。这是一道“爱情问题”：

假设你一生中能且只能交三个女友，且你必须遵守以下规则：

1. 不得脚踏两只船；
2. 不得吃回头草。

那么，应该以怎样的策略进行选择，才能够尽可能地选择到最好的伴侣呢？

如果你只认准了第一个，那么有 1/3 的机率选择到最好的。同理，只认准第二个或第三个也是 1/3 机率。比较好的策略应该是：

• 果断放弃第一个；
• 如果第二个比第一个好，就选择第二个；
• 否则，选择第三个。

通过简单的排列试验，就可以发现，这种策略有 1/2 机率选择到最好的，有 1/3 机率选择到中等的，有 1/6 机率选择到最差的。比瞎蒙的三足鼎立要更安全一些。当然，对于不少人来说，初恋是无条件的最好的。那就不是这个简单的模型能解释的了。

回到那道复杂一些的“钻石问题”上来。“钻石问题”跟“爱情问题”原理类似，只是参数从 3 变成了 10。类似地，最佳策略的格式应该是这样的：

• 放弃前 \(x\) 个；
• 拿下此后第一个出现的比前 \(x\) 个都要大的钻石。

只需要找出这样的 \(x\)，使拿到最大一颗钻石的机率 \(p(x)\) 取到最大值。为此，我们需要写出 \(p(x)\) 的表达式。

为了使讨论不失一般性，将钻石的总数（也就是楼层总数）记为 \(N\)，每颗钻石由小到大分别记为 \(1, 2, \ldots, N\)。现在来写出 \(p(x)\) 的表达式。

将前 \(x\) 颗钻石中最大的一颗记为 \(i\)，可知 \(i\in [x,N]\)。倘若 \(i=N\)，则无论如何都拿不到最大一颗钻石。先排除这种情况。

再来看剩余的 \(N-x\) 颗钻石。在这些钻石中，有 \(N-i\) 颗比 \(i\) 大的钻石（当然其中包括最大的一颗）。只有当最大的一颗钻石排在这 \(N-i\) 颗钻石的第一位时，我们才能选择到它，因此，在前 \(x\) 颗钻石中最大号为 \(i\) 的前提下，我们有 \(p_2(x,i) = 1/(N-i)\) 的机率选择正确。

现在需要算一下前 \(x\) 颗中最大号为 \(i~(i\in [x, N-1])\) 的机率 \(p_1 (x,i)\) 。先从所有比 \(i\) 小的 \(i-1\) 颗钻石中选出 \(x-1\) 颗进行排列，再将 \(i\) 号钻石加入其中，这一共有 \(x \cdot P^{x-1}_{i-1}\) 种可能。而总可能数为从 \(N\) 颗钻石中选出 \(x\) 颗进行排列。因此，得到：\(p_1(x,i) = x \cdot P^{x-1}_{i-1} / P_N^x\)。

最终的概率：\(p(x) = \sum\limits_{i=x}^{N-1} p_1(x,i)\cdot p_2(x,i)\)

把 \(x\) 从 \(1\) 试到 \(N-1\)，找出 \(p(x)\) 的最大值即可。对于此题 \(N=10\)，借助 Excel 就可以方便地求出结果：

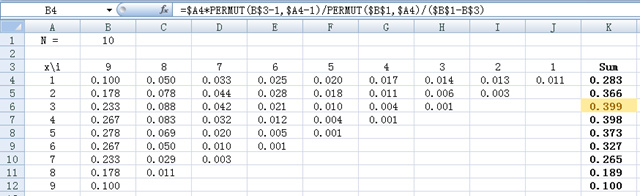
可以看出，当 \(x=3\) 时，取得最大钻石的机率最大。也就是说，前三颗钻石放弃，之后只要有比那三颗大的就拿。也就是说：如果你打算交够十个女友，那么前三个可以放弃，之后……

……就会发现一个不如一个了。